Bayes-Ball
Suppose you are a longtime Red Sox fan and you just bought a ticket to the fourth of a four-game series against the Yankees. The Red Sox have won two of the three previous games in the series. As you settle into your seat at Fenway, everyone around you is confident the Red Sox will win. At least that’s the best bet. But what are the odds on that bet? Even if you are loathe to bet on the Yankees, what is the chance the Red Sox lose?
The Red Sox have won two out of the three previous games, so it is reasonable to think that the probability that they win the next game is percent. But maybe the Red Sox’ win probability against the Yankees is actually higher, say percent, and they just got unlucky in the first game. Or maybe the Red Sox’ win probability is actually lower— or even percent—and they just happened to be on a hot streak. Guessing percent seems reasonable, but how do we know this is even a good estimation scheme?
Suppose we only watched the first game, which the Red Sox lost. If we used the same estimation scheme, then we’d be forced to say that the Red Sox have a percent win chance in any future game. This is clearly not a reasonable guess since there has to be some chance that the Red Sox win. One game does not provide enough information to make this estimator reasonable. Why? Because we’ve seen the Red Sox win other games and we know even the best MLB teams don’t have a percent win probability against the worst teams.
This statement—no team has a percent win probability against any other team—is an example of prior knowledge. We know something about baseball before we see any games. This prior knowledge lets us reject simple estimation schemes when they give answers that are wildly off-base. Can we use prior knowledge to improve our estimator so that it doesn’t go foul?
Questions
The story above raises three main questions:
- How should we estimate the win probability of team 1 against team 2 if we see team 1 win out of games against team 2?
- How can we incorporate prior information about baseball to improve this estimate?
- What prior information do we actually have about win probabilities in baseball?
The answers to all three of these questions depend on one number, . The value of represents our prior knowledge about baseball. It is large when teams are often evenly matched (win probabilities near percent) and small when teams are often unevenly matched (win probabilities near or percent). A large means most games are unpredictable; a small means most games are predictable.
Given , there is a surprisingly simple way to estimate win probabilities that accounts for prior knowledge. This method can be motivated rigorously while remaining easy to compute. It is so easy to compute that you could use it while sitting in the bleachers with Cracker Jacks in one hand and a hot dog in the other.
But to use this method you need to know . In this article, we fit for based on the history of baseball. By estimating , we gain insight into the nature of the sport and how that nature has changed over the league’s 148-year history.
How to Incorporate Prior Information
Before we get to , we need to understand the question we are asking. Specifically, how to balance prior knowledge with observed games and arrive at a probability.
To do this we need some notation. Capital letters are used for quantities that are either random or unknown while lower case letters are used for quantities that are either fixed or known.
Let be the number of games observed and be the number of games team 1 won. Since there is a chance that either team could win or lose any game, observing wins is a specific outcome out of many possible outcomes. Let be a random variable representing the number of wins if we could run the games again. This is analogous to seeing a coin land heads times out of flips. is the number of times it lands heads if we flip more times. Let be the probability that team 1 beats team 2. Assume that this probability is independent of the outcome of all previous games and is constant over the course of the games.
In order to estimate , we want to know the likelihood that given that for any possible outcome . We could then find what win probability is most likely given the observed outcome. The likelihood that given is the conditional probability: .
Throughout this article we will use $\text{Pr}\{A\}$ to denote the probability that event $A$ occurred. For example, $\text{Pr}\{W = w\}$ is the probability that the number of wins, $W$, is equal to $w$.
The joint probability that two events occur is the probability they both occur. For example, the probability that a randomly-drawn American is male and over 6 feet tall is the joint probability of the event that the American is male and the event that the American is six feet tall. Joint probability is indicated with the intersection sign $\cap$. The $\cap$ can be read as “and.” For example:
$$\text{Pr}\{\text{male and over six feet} \} = \text{Pr}\{\text{male} \cap \text{over six feet}\}.$$
Conditional probability is the probability an event occurs given that another has occurred. For example, the probability an American man is over six feet tall is the conditional probability that an American is over six feet tall given that he is a male. Conditional probability is denoted with a vertical bar $|$. The $|$ can be read as “given that.” For example:
$$\text{Pr}\{\text{over six feet given male} \} = \text{Pr}\{\text{over six feet}|\text{male}\}.$$
Joint and conditional probabilities are related by the fact that the probability that two events occur, $A$ and $B$, is the probability $B$ occurs given $A$ occurs times the probability $A$ occurs. In notation:
$$\text{Pr}\{A \cap B\} = \text{Pr}\{B|A\} \text{Pr}\{A\}.$$
In our example, 14.5 percent of American men are over 6 feet and 49.2 percent of Americans are male. Therefore:
$$\text{Pr}\{\text{male} \cap \text{over six feet}\} = \text{Pr}\{\text{over six feet}|\text{male}\} \text{Pr}\{\text{male}\} = 0.145\times 0.492 = 0.071.$$
This equation can also be used to solve for conditional probabilities from joint probabilities:
$$\text{Pr}\{B | A\} = \frac{\text{Pr}\{B\cap A\}}{\text{Pr}\{A\}}.$$
To find this conditional probability, we will use Bayes’ rule.
Bayes’ rule expresses the probability that a random event occurs given that occurred in terms of the odds that occurs given that occurred. It reverses the direction of the conditioning. This reversal is useful because conditional probabilities are often easier to work out in one direction than in the other. Bayes’ rule comes from the following pair of equalities:
Setting the two equal to each other and solving for yields:
Bayes’ rule is a method for computing the conditional probability of an event based on observations of a different, but related, event. For example, suppose that you and I play a game of dice in which the high roller wins. Given that you win, what is the probability that you rolled a five?
Let’s first find the joint probability that you rolled a five and won. The probability that you rolled a five is $1/6$. The probability that you won with a five is $4/6$, since you cannot have won if I rolled a five or six. Therefore, the joint probability is:
$$ \text{Pr}\{\text{win} \cap \text{rolled a 5}\} = \text{Pr}\{\text{win} | \text{rolled a 5}\} \text{Pr}\{\text{rolled a 5}\} = \frac{4}{6} \times \frac{1}{6} = \frac{4}{36}. $$
Here we have computed the joint probability in the direction of causality. There is a probability you rolled a five; given that you rolled a five, there is another probability that you won. Bayes’ rule works by going against causality. It is equally true that:
$$ \text{Pr}\{\text{win} \cap \text{rolled a 5}\} = \text{Pr}\{\text{rolled a 5} | \text{win}\} \text{Pr}\{\text{win}\}. $$
Notice that $ \text{Pr}\{\text{rolled a 5} | \text{win}\} $ is the conditional probability we were originally looking for. Thus, if we divide across by the probability that you win, we get:
$$ \text{Pr}\{\text{rolled a 5} | \text{win}\} = \frac{\text{Pr}\{\text{win} \cap \text{rolled a 5}\}}{\text{Pr}\{\text{win}\}}. $$
We can then substitute in our original expression for the joint probability that appears in the numerator:
$$ \text{Pr}\{\text{rolled a 5} | \text{win}\} = \frac{\text{Pr}\{\text{win} | \text{rolled a 5}\} \text{Pr}\{\text{rolled a 5}\}}{\text{Pr}\{\text{win}\}}. $$
This gives the conditional probability going backwards in terms of the conditional probability going forwards. We already know what the numerator is because we know the conditional probability going forwards: $4/36$.
To compute the denominator, you have to find the overall probability that you win, which is: [the probability you win and rolled a $1 $] $+$ [the probability you win and rolled a $2 $] $+$ [the probability you win and rolled a $3 $], and so on up to $6$. In mathematical terms:
$$ \begin{aligned} \text{Pr}\{\text{win} \} & = \sum_{x = 1}^{6} \text{Pr}\{\text{win} \cap \text{rolled a } x\} \\ & = \sum_{x = 1}^{6} \text{Pr}\{\text{win} | \text{rolled a } x\} \text{Pr}\{\text{rolled a } x\} \\ & = \sum_{x = 1}^{6} \frac{(x - 1)}{6} \frac{1}{6} = \frac{0 + 1 + 2 + 3 + 4 + 5}{36} = \frac{15}{36}. \end{aligned} $$
Putting it all together:
$$ \text{Pr}\{\text{rolled a 5} | \text{win}\} = \frac{\text{Pr}\{\text{win} | \text{rolled a 5}\} \text{Pr}\{\text{rolled a 5}\}}{\text{Pr}\{\text{win}\}} = \frac{4/36}{15/36} = \frac{4}{15}. $$
Note that the probability you rolled a five given that you won, $4/15$, is greater than the probability of rolling a five, $1/6$. This is because you are more likely to win if you roll a large number. Knowing that you won suggests you rolled a high number.
For another example of Bayes’ rule in action, check out our article on snow leopards.
Applying Bayes’ rule to our problem gives:
The conditional probability on the left hand side, , is the posterior. This is the probability that the given that team 1 won out of games. It is called the posterior because it is the distribution of win probabilities after observing data. Our goal is to find the probability that maximizes the posterior.
On the right hand side, , is the likelihood, so named because it is the likelihood of observing the data given a win probability . The probability is the prior. This is the probability that team 1 has a win probability against team 2 before we observe any games between them. We’ve done it! This is how we incorporate prior knowledge.
The Prior
Now that we know how to incorporate prior knowledge, what do we want it to be? What distribution should we use to model the probability that a baseball team has win probability against another team?
We will use a symmetric beta distribution since the beta distribution is the standard choice for this type of estimation problem (don’t worry, the reasons will become apparent once we start the analysis). This is where enters; it is the parameter that defines this distribution.
When , the distribution is uniform—all win probabilities are equally likely. This is the same as knowing nothing about the win probabilities. When , the distribution is a downward-facing parabola. When , the distribution is bell-shaped. The larger , the more the distribution concentrates about . In essence, a large means less predictable games and a more competitive league. You can experiment with different s below.
The more concentrated the distribution, the less likely it is that team 1 has a large (or small) win probability against team 2. Therefore, by tuning we can express our expectation about how even baseball teams are. We will use past baseball data to fit for this parameter. Note that this prior does not incorporate prior information about specific teams, only about the nature of baseball as a whole.
The Estimator
Now we can state our original question formally. If team 1 wins out of games against team 2, and if the win probabilities are sampled from a beta distribution with parameter , then what is the most likely win probability for team 1?
This may seem like a hard question to answer cleanly—and in general it is. However, by picking the beta distribution as our prior, the answer becomes both elegant and intuitive.
The most likely win probability , having seen wins out of games, given prior parameter , is:
This win probability maximizes . That’s all there is to it!
What makes this so brilliant is that the parameter can be treated as a number of fictitious games. Think back to our original method for estimating the win probability: the win frequency (ratio of wins to games played). The most likely win probability is just the win frequency if we pretend that our team wins more games and loses more games.
For example, suppose that , , and . Instead of estimating that the Red Sox have a win probability, we estimate that they have win probability , just as if they had won and lost one more game. If instead , then our estimated win probability would be the Red Sox’ win frequency had they won an additional 4 games and lost an additional 4 games: .
Notice that as grows, the estimated win probability approaches . As a consequence, if is large, then our estimator is conservative, and it will take a lot of games to move the estimated win probability far away from .
You can experiment with different , , and s below. While you experiment, consider how large you think should be for baseball.
Gives a win probability of 0.656
The proof that maximizes the posterior is included below (in two pieces). The proof is not necessary to understand the role of in the estimator; however, it is important to understand why the estimator takes this form. In particular, the proof below is needed to understand exactly what is assumed a priori about baseball win probabilities given a particular . The motivation for the beta prior is explained in the second half of the proof. That said, if you are only interested in how has changed over time and how differs between different sports, skip to the end of the proof and continue from there.
Proof Without Prior ()
Why does the most likely win probability take this form?
If we do not incorporate prior information, then the posterior is proportional to the likelihood and maximizing the posterior is equivalent to maximizing the likelihood. To find the likelihood, condition on (assume that the win probability is ). Then the number of wins is binomially distributed, which means that:
Why the binomial distribution?
Suppose that two teams played five games, and that team $ A $ won the first two games, lost the third, won the fourth, and lost the fifth. They won three games and lost two. With a $p$ probability of winning each game, the probability they won those exact three games is $ p \times p \times p = p^3 = p^w $. Then the probability they lost two games is $ (1-p) \times (1-p) = (1-p)^2 = (1-p)^{n-w}$, since the probability of losing any one game is $1 - p$. Thus the probability of this particular sequence of wins and losses is $p^3 (1-p)^2 = p^{w} (1-p)^{n-w} $. The same is true for any sequence of three wins and two losses. This explains the part of the binomial distribution that depends on $p$.
The prefactor in the front of the binomial accounts for the fact that there are multiple different sequences of wins and losses that have the same total number of wins. In our example, the sequences $WWWLL$, $WWLWL$, $WWLLW$, $WLWWL$, $WLWLW$, $WLLWW$, $LWWWL$, $LWWLW$, $LWLWW$, and $LLWWW$ all have the same number of wins and losses. The sequences are all equally likely and occur with probability $p^{3}(1-p)^{2}$. If we had only specified that three wins occurred, then any of these ten sequences might have happened. Therefore, the probability that three wins occurred is ten times the probability of any particular sequence. This is what the prefactor, or multiplicity, represents: the number of different sequences of $n$ games with $w$ wins.
To compute the multiplicity we use the "choose" operation:
$$ \left(\begin{array}{c} n \\ w \end{array} \right) = \frac{n!}{w!(n-w)!} = n \text{ choose } w $$
where $n! = n \times (n-1)\times (n-2) . . . 3 \times 2 \times 1$. The choose operation is used since drawing sequences of $w$ wins and $n - w$ losses is an example of a combination.
Going back to our example of five games and three wins: there were ten different sequences, and $ 5!/(3!(5-3))! = 120/((6)(2)) = 10 $, so $5$ choose $3$ is the multiplicity, $10$.
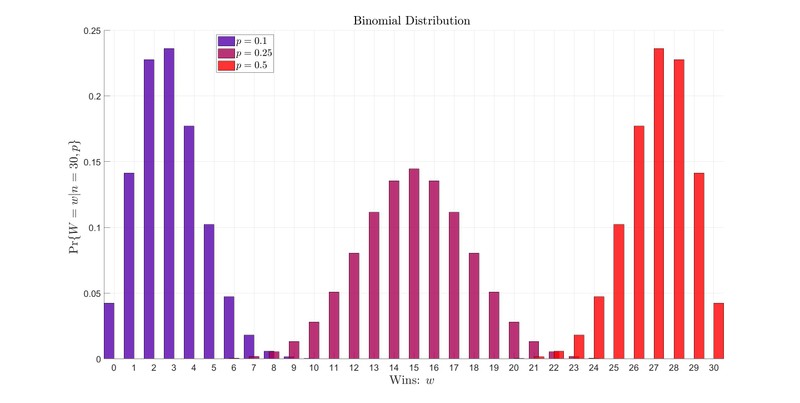
So in the absence of prior information:
Note that is not binomially distributed because the posterior is a distribution over not . When using the expression on the right as a posterior it is important to remember that is the variable that can change and and are fixed by what happened in the observed games.
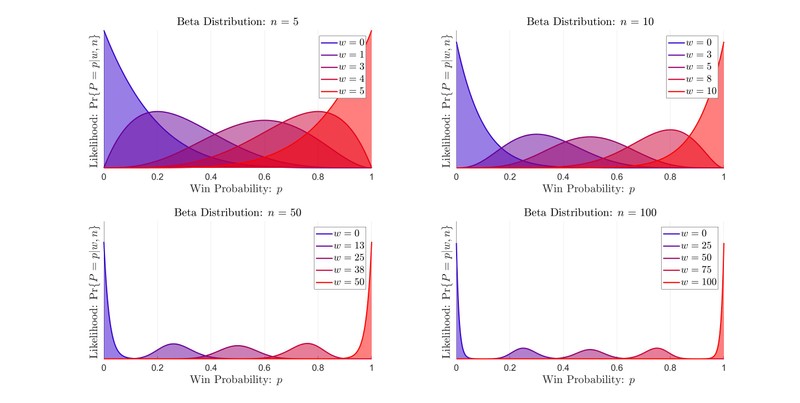
This distribution is an example of a beta distribution. A beta distribution is a probability distribution for probabilities. It is often used to give the probability . The beta distribution depends on two parameters, . It has the form: 1
where:
and is the gamma function. The gamma function is the continuous extension of the factorial. That is: for any integer , but, unlike the factorial, is defined for all real . It follows that if and are integers, then equals choose . Therefore, our likelihood is beta-distributed with parameters equal to the number of wins, , and losses, :
The likelihood allows us to calculate the probability that having observed wins out of games (in the absence of prior information). What win probability, , maximizes the likelihood?
To maximize the likelihood we maximize the log-likelihood. Since a logarithm is monotonically increasing in its argument the log-likelihood is maximized wherever the likelihood is maximized. The log-likelihood is:
Differentiating with respect to :
Setting the derivative to zero requires or:
This is solved when . The win frequency is the only solution to this equation, so the log-likelihood has one extremum. The log-likelihood is a convex function, so this extremum is a maximum. Thus the win probability that maximizes the likelihood is the win frequency:
This is a good motivation for our naïve estimation scheme. If the Red Sox win two out of three games then we guess that their win probability is . This, however, is the solution without any prior information. It is equivalent to the solution when we assume that all win probabilities are equally likely. As noted before, this solution breaks down if or since it returns either a or percent chance of victory in future games. What we need is a prior distribution that can be fit to baseball data so the estimator does not return extreme win probabilities.
Proof Incorporating the Prior ()
In order to incorporate a prior we need to pick a form for the prior distribution, . The classic choice of prior for this problem is our home favorite, the beta distribution. The beta distribution is the standard choice of prior for this problem because it is the conjugate prior to the binomial distribution.
A conjugate prior is a distribution that, when chosen as a prior, ensures that the posterior distribution has the same form as the likelihood, only with different parameters. In our case, if we use a beta distribution as a prior, then the posterior is also beta-distributed, only with different parameter values. These parameters depend on both the data observed and the parameters of the prior.
Recall that the beta distribution depended on two parameters, and . In our case we require that our prior is symmetric about , because if team 1 has a win probability of against team 2, then team 2 has a win probability of against team 1. If we did not assume the prior was symmetric in this way, then the probability a team wins against another would depend on the order we listed them in. Requiring that the beta distribution is symmetric requires . This means that our prior only depends on one parameter and has the form:
The product is a downward facing parabola that is maximized at and equals zero at and . Changing bends this parabola. For the parabola gets bent down into a bell shape. For the parabola is bent up towards a box. At the box becomes the uniform distribution. This effect was illustrated in Demo 1.
When symmetric, the beta distribution has mean and variance . Therefore, as goes to infinity the variance in the beta distribution vanishes. In that case almost all of the win probabilities are expected to be close to . This leads to the simple intuition:
- Large win probabilities near unpredictable games, even teams, competitive league
- Small win probabilities can be near or more predictable games, uneven teams, less competitive league
How does introducing this prior change our estimator?
The maximum likelihood estimator (MLE) is the probability that maximizes the likelihood. The maximum a posteriori estimator (MAP) is the probability that maximizes the posterior. Using a symmetric beta distribution with parameter sets the posterior proportional to:
As promised, the posterior has the same form as the likelihood, only now the parameters are and . Therefore, by using a beta prior, the posterior distribution takes the same form as the likelihood had we seen an additional wins and losses. The parameter is, in effect, the number of fictitious games added to the record when accounting for prior information. Symbolically:
Since we already know how to maximize the likelihood, we also already know how to maximize the posterior. The likelihood is maximized at the win frequency so the posterior is maximized at the win frequency—after wins and losses have been added to the record:
The estimator we propose here is the maximum a posteriori estimate (MAP). It maximizes the posterior distribution and thus is the most likely win probability given the data.
An alternative point estimator is the expected win probability given the posterior. This is:
$$ \begin{aligned} p_{e}(w,n|\beta) & = \int_{0}^{1} p \text{ posterior}(p|w,n,\beta) dp \\ & = \frac{1}{B(w + \beta + 1, n - w + \beta + 1)}\int_{0}^{1} p p^{w + \beta} (1-p)^{n - w + \beta} \\ & = \frac{1}{B(w + \beta + 1, n - w + \beta + 1)}\int_{0}^{1} p^{w + \beta + 1} (1-p)^{n - w + \beta} \\ & = \frac{B(w + \beta + 2,n - w + \beta + 1)}{B(w + \beta + 1, n - w + \beta + 1)} \end{aligned} $$
To simplify we use the fact that $B(\alpha,\beta) = \Gamma(\alpha) \Gamma(\beta)/\Gamma(\alpha + \beta)$. Since $\Gamma$ is the continuous extension of the factorial, this is essentially the continuous extension of the choose operation. Substituting in:
$$ \begin{aligned} p_{e}(w,n|\beta) & = \frac{B(w + \beta + 2,n - w + \beta + 1)}{B(w + \beta + 1, n - w + \beta + 1)} \\ & = \frac{\Gamma(w + \beta + 2) \Gamma(n - w + \beta + 1) \Gamma(n + 2 \beta + 2)}{\Gamma(n + 2 \beta + 3) \Gamma(w + \beta + 1) \Gamma(n - w + \beta + 1)} \\ & = \frac{\Gamma(w + \beta + 2) \Gamma(n + 2 \beta + 2)}{ \Gamma(w + \beta + 1) \Gamma(n + 2 \beta + 3)}. \end{aligned} $$
Much like the factorial, the $ \Gamma $ function obeys the recursion: $ \Gamma(x + 1) = x \Gamma(x) $. Thus $\Gamma(x+1)/\Gamma(x) = x $. Plugging in:
$$ p_{e}(w,n|\beta) = \frac{\Gamma(w + \beta + 2) \Gamma(n + 2 \beta + 2)}{ \Gamma(w + \beta + 1) \Gamma(n + 2 \beta + 3)} = \frac{w + (\beta + 1)}{n + 2 (\beta + 1)}. $$
The expected win probability given $w$ wins, $n $ games, and prior parameter $ \beta $ is the same as the win frequency had team 1 won and lost an additional $ \beta + 1 $ games against team 2. Note that if $\beta = 0 $, then we add one additional win and loss to the record in order to estimate the win probability. This is the famous Laplace Rule of Succession 2.
One way to measure the uncertainty in our estimate is with the variance (or standard deviation) in the posterior distribution. The variance of a beta distribution with parameters $ \alpha $ and $\beta $ is:
$$ \text{Var} = \frac{(\alpha + 1)(\beta + 1)}{(\alpha + \beta + 2)^2(\alpha + \beta - 1)}. $$
Our posterior is a beta distribution with parameters $w + \beta$ and $n - w + \beta$. Therefore the uncertainty in our estimator is:
$$ \text{Var}(P) = \frac{(w + \beta + 1)(n - w + \beta + 1)}{(n + 2 \beta + 2)^2(n + 2 \beta - 1)}. $$
And the standard deviation in our estimator is:
$$ \text{std}(P) = \sqrt{\frac{(w + \beta + 1)(n - w + \beta + 1)}{(n + 2 \beta + 2)^2(n + 2 \beta - 1)}}. $$
Notice that the bottom is cubic in the $ n $ and $ \beta $ while the numerator is quadratic in each. As a result, the standard deviation in the posterior decays proportional to $ n ^{-1/2} $ or $ \beta^{-1/2} $ as might be expected. This means that to reduce the uncertainty in the posterior by some factor $ \epsilon $ we need to observe about $ \epsilon^{-2} $ games. We might reasonably hope to get our estimate of the win probability to within 10 percent. This requires seeing on the order of 100 games. We therefore expect to have significant uncertainty in our estimate of the win probabilities until we have seen many games (or unless $ \beta $ is very large).
and the Nature of Baseball
We now have an intuitive way to incorporate prior information about the win probabilities into our estimate for the win probability given data. What remains is to have an estimate for (now that we know how to use prior information we need to gather the prior information).
In order to estimate we need to:
- gather historical baseball data to use in the estimate
- work out an estimation framework for estimating given the data
FiveThirtyEight provide the score of all 220,010 MLB games played since 1871 here.3 This data can be used to estimate for every year of Major League Baseball. In order to smooth the results, we fit for on sliding ten-year intervals (i.e., we find the best fit for for 2010 to 2019, 2009 to 2018, and so on back to the decade spanning from 1871 to 1880). These intervals are indexed by the last year in the interval so that our estimate for in 2019 is based on all the years between 2010 and 2019. This way the estimate for in a given year does not depend on games that have not yet occurred.
To fit for we used a Bayesian estimation framework much like the framework derived in this article for estimating the win probability. We did not assume any prior information about and solved for the value of that maximized the likelihood of given the corresponding decade of baseball. As before, this likelihood was solved for by first finding the likelihood of sampling the observed decade of baseball conditioned on a given . Then the likelihood of given the decade was computed using Bayes’ rule. Formally, this likelihood is the product of a series of beta-binomial distributions. Details are included in the expandable box below.
Ok, so how do we actually do this estimate?
The conceptual setup is the same as what we’ve already done only for a new estimation problem. This time our data comes as a number of wins out of a number of games between each pair of teams each year. Let $y$ be the year and let $i,j$ be the two teams. Then we have $w_{ij}(y)$ and $n_{ij}(y)$ for all 148 years of Major League Baseball (MLB).
We consider a decade at a time, which means we let the final year, $y_{final}$, range from 1880 to 2019 and for each $y_{\text{final}}$ consider only data from the range of years $y = [y_{\text{final}}-9,y_{\text{final}}] $.
Pick a decade to consider, say $y_{\text{final}} = 2009 $. Now, we want to compute the posterior distribution for $\beta(2009)$. Since we have no prior expectation about $\beta$, this is proportional to the likelihood. Using Bayes’ rule, the likelihood of a given $ \beta $ equals the likelihood of sampling $w_{ij}(y)$ given $n_{ij}(y)$ for all pairs of teams and for all years in the decade if all the win probabilities are sampled from a beta distribution with parameter $ \beta $.
To compute this likelihood we assume that the outcome of each game is independent of the outcome of every other game and that the win probability of team 1 against team 2 is fixed over the course of a year. Then, for each $(i,j,y)$, there is a win probability $P_{ij}(y)$ sampled from the beta distribution. What we need is the probability of sampling $w_{ij}(y)$ given $n_{ij}(y)$ if $P_{ij}(y)$ is sampled from a beta distribution with parameter $ \beta $. That probability is given by the beta-binomial distribution:
$$ \text{Pr}\{W = w|n,\beta\} = \frac{B(w + \beta + 1,n - w + \beta + 1)}{B(\beta + 1,\beta + 1)} $$
This result can be achieved by noting that this is equivalent to the marginal distribution that $W = w$:
$$ \text{Pr}\{W = w|n,\beta\} = \int_{p =0}^{1} \text{Pr}\{W=w|n,p\} \text{Pr}\{P = p|\beta\} dp \propto \int_{p=0}^{1} p^{w + \beta} (1-p)^{n + w + \beta} dp. $$
The integral is proportional to $B(w + \beta + 1,n - w + \beta + 1)$, and the denominator is inherited from the normalization factors.
Then, using Bayes’ rule:
$$ \text{Pr}\{\beta|\text{history from decade}\} = \prod_{i,j,y \in \text{decade}} \frac{B(w_{ij}(y) + \beta + 1,n_{ij}(y) - w_{ij}(y) + \beta + 1)}{B(\beta + 1,\beta + 1)} $$
To find the best fit $ \beta $ we search for a $\beta$ that maximizes this likelihood. This is done by computing the log of the likelihood and then using a numerical optimizer. The numerical optimizer is initialized by evaluating the log-likelihood at a series of sample points spaced geometrically between $10^{-3}$ and $10^{3}$. The sample with the largest log-likelihood is then used as the initial guess at $\beta$. Once the MLE has been found we find a probability $p$ such that there is a 95 percent chance of sampling $\beta $ from the interval where the likelihood is greater than or equal to $p$.
We also computed the 95 percent confidence interval on our estimate for using the same likelihood. If baseball win probabilities are beta-distributed, then there is a 95 percent chance that is in the interval if it is sampled from its posterior.
The results of this analysis are shown in Figure 3.
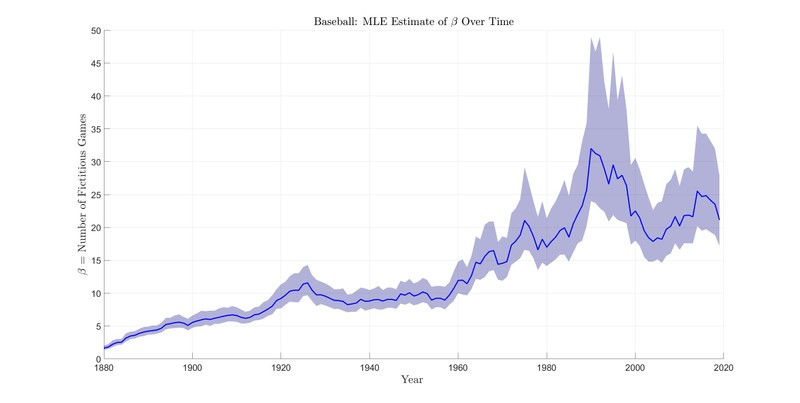
The average results for each decade are provided in Table 1.
| Decade | 95% Lower | MLE | 95% Upper |
|---|---|---|---|
| 2010–2019 | 17.4 | 21.9 | 30 |
| 2000–2009 | 14.9 | 18.8 | 25.4 |
| 1990–1999 | 20.6 | 27.3 | 41.2 |
| 1980–1989 | 15.2 | 19.3 | 26.2 |
| 1970–1979 | 13.5 | 16.8 | 22.2 |
| 1960–1969 | 10.6 | 13 | 16.6 |
| 1950–1959 | 7.1 | 8.6 | 10.7 |
| 1940–1949 | 6.8 | 8.2 | 10.1 |
| 1930–1939 | 6.5 | 7.8 | 9.6 |
| 1920–1929 | 7.6 | 9.3 | 11.7 |
| 1910–1919 | 5.1 | 6.1 | 7.3 |
| 1900–1909 | 4.2 | 5.2 | 6.4 |
| 1890–1899 | 3.3 | 4 | 4.9 |
| 1880–1889 | 1.4 | 1.9 | 2.5 |
Using this table we can easily compute the MAP estimate for the win probability of a baseball team that won out of games in any decade. For example, if the Red Sox beat the Yankees 2 out of 3 games in 1885 (ignoring that neither team existed at the time), then the MAP estimator for the win probability would be . Alternatively, if we saw the same thing today, the MAP estimator would be . Seeing the Red Sox win 2 out of 3 games only makes our estimate percent larger than percent!
Tragically, the Yankees won 14 out of 19 games against the Red Sox in 2019, which means our best estimate for the Red Sox win probability against the Yankees in 2019 is . This is still shockingly close to percent given that the Red Sox’ win frequency against the Yankees in 2019 was only .
These examples illustrate how astonishingly large is for modern baseball. Modern baseball teams have proven to be fairly even, so we expect most team against team win probabilities to be near . The beta distribution with is shown below in Figure 4. Note that very few teams are expected to have a win probability greater than percent against any other team. This means that most matchups are relatively fair and fairly unpredictable.
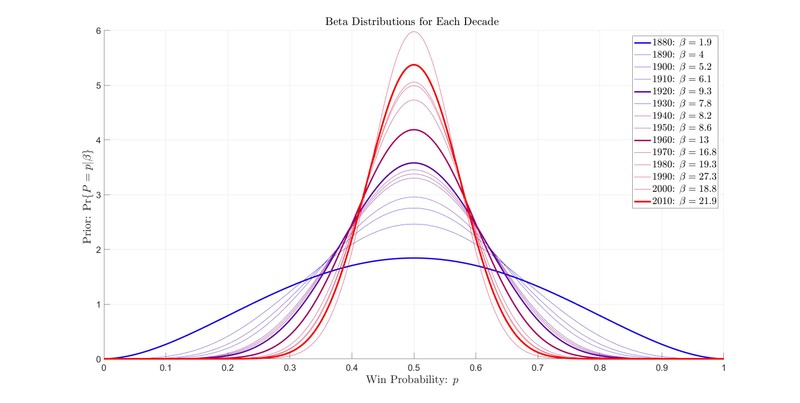
The astonishing evenness of modern baseball is reflected in how large is. With it would take winning eleven games straight to push the estimated win probability above and forty-four games straight to push it past . The median number of games played between pairs of teams who competed in 2019 was seven games, and the max was nineteen, including playoffs. Few teams even play enough games to push the estimate past percent or beneath percent. Note that is so large that in all cases we add more fictitious games to the estimator than we do real games.
Baseball wasn’t always this even. Take a look back at Figure 3 and notice the gradual increase in over time. At the start of the league, is less than one. In fact, in 1880 the MLE estimate for is (with a confidence interval ). The gradual increase in over the history of the league reflects the league becoming more competitive. Over time teams have become more even and the playing field more level. It is now so level that it takes over twenty games—more games than are played between almost any pair of teams—before observed data has a bigger influence on our estimate than our prior expectation does.
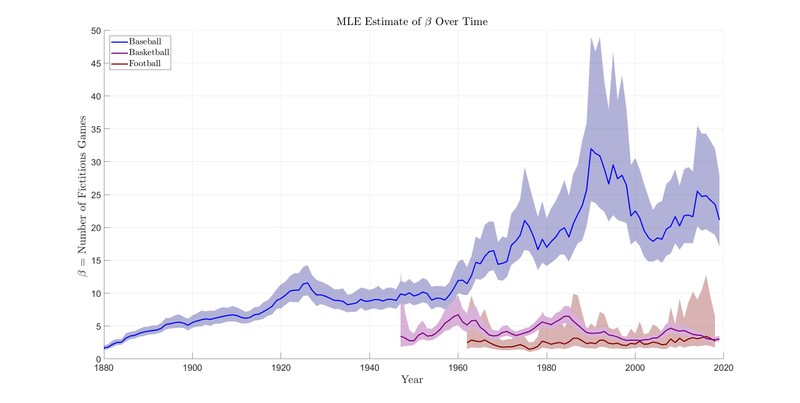
Unlike the MLB, both the NBA and NFL have had close to constant s over time. Both also have much smaller s than the MLB. For example, in the 2010s the NBA and NFL have s equal to and games respectively. This indicates that both the NFL and NBA are far more predictable than baseball, and football and basketball teams are far less evenly matched than baseball teams.
For example, if we saw the Celtics beat the Knicks 2 out of 3 games, we would estimate the Celtics win probability was . The same situation in baseball would lead to a predicted win probability of . For a more extreme example, imagine the Celtics and Red Sox each win 9 out of 10 games against the Knicks and Yankees respectively. The best estimate of the Celtics’ win probability is while the best estimate for the Red Sox’ is . The Celtics’ win probability is only less than their win frequency, , while the Red Sox’ is less than .
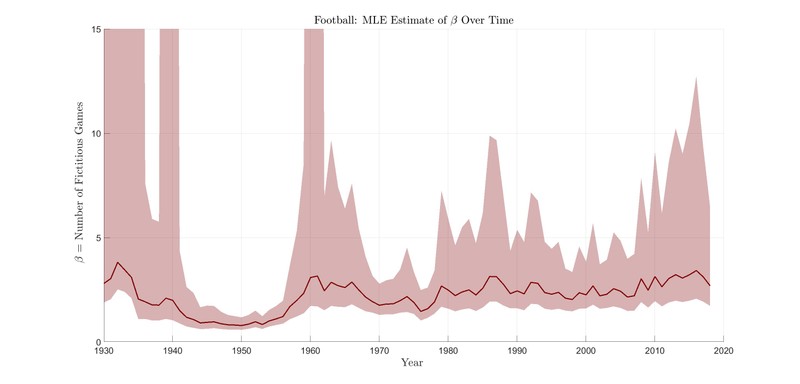
It is also interesting to note that the likelihood distribution for skews much more positive for football than for basketball or baseball. This is because football teams play far fewer games per pair and much less data is available for fitting to any decade of NFL games. The median number of games played between any pair of NFL teams who competed with each other in 2018 was one game and the max was three. Any pair of teams who play only one game do not provide any information for estimating , so the estimate of is limited to pairs of teams who play two or more games (teams within a division play twice against each possible opponent, and teams may meet more than once if they play in the regular season and in the playoffs). The uncertainty in football is most dramatic in the very early years of the league, when there were more teams and fewer games per pair, and in the 1960s, when the AFL joined the NFL (see Figure 6).
Full results for basketball and football are provided below in Table 2.
| Decade | 95% Lower NBA | MLE NBA | 95% Upper NBA | 95% Lower NFL | MLE NFL | 95% Upper NFL |
|---|---|---|---|---|---|---|
| 2010–2019 | 2.1 | 2.5 | 3.2 | 0.9 | 2.1 | 8.1 |
| 2000–2009 | 2 | 2.5 | 3.1 | 0.6 | 1.4 | 3.9 |
| 1990–1999 | 2.1 | 2.5 | 3.1 | 0.6 | 1.4 | 4 |
| 1980–1989 | 3.6 | 4.5 | 5.7 | 0.7 | 1.6 | 5.4 |
| 1970–1979 | 2.7 | 3.3 | 4.1 | 0.3 | 0.9 | 2.6 |
| 1960–1969 | 2.9 | 3.9 | 5.5 | 0.6 | 1.6 | 5.3 |
| 1950–1959 | 2.4 | 3.3 | 5 | -0.1 | 0.3 | 1.8 |
| 1940–1949 | 0.9 | 2.1 | 7.2 | -0.3 | 0.1 | 1.1 |
| 1930–1939 | 0.6 | 1.6 | 5.4 |
Taken together, these estimates of tell a story about the nature of these leagues. It is clear that baseball is an outlier when compared to the NFL and the NBA. Not only is the league much older and not only do baseball teams play far more games, but baseball teams are more evenly matched than football or basketball teams, and baseball teams have gotten more evenly matched over time. You would have to go back to 1880 (or at least 1900) for the teams in MLB to be as unevenly matched as the teams in professional football or basketball. Baseball is now so even that it is difficult to estimate teams’ win probabilities against each other without seeing close to twenty games between them. Until then, your estimates are more informed by than the games you watched. Until then, your estimates are more Bayes'-ball than baseball.
-
This is not quite the standard parameterization of the beta distribution. The beta distribution is usually defined with set to what we call and set to what we call . We chose to modify the convention to ease interpretation of the parameters.
↩ -
Laplace, Pierre-Simon. "Philosophical essay on probability. 2nd ed." Paris: Mrs. Ve Courcier (1814).
↩ -
All data was collected from https://data.fivethirtyeight.com/↩